Self-avoidance is similar to intoxication, at least in the world of algorithms where an agent traverses a space.
A random, or drunkard’s walk can be concieved of an agent traversing a 2D space, each step at random, and in this case orthogonally for simplicity reasons. Simple enough to implement such an agent that moves around with equal probability.
class Agent {
float x, y;
Agent(float x, float y) {
this.x = x;
this.y =y;
}
void display() {
strokeWeight(.5);
point(x, y);
}
void move() {
//cf https://natureofcode.com/book/introduction/
int choice = int(random(4));
if (choice == 0) {
x++;
stroke(#FFC482);
} else if (choice == 1) {
x--;
stroke(#496A81);
} else if (choice == 2) {
y++;
stroke(#66999B);
} else {
y--;
stroke(#B3AF8F);
}
}
}
Unmodified random walks can be interesting, but for most part the unconstrained random movement appears to my eye like uninteresting noise, even with a couple of aesthetic decisions (light strokeweight and varying colors from a palette thrown in). Here is an output after a million random steps.

At the addition of single simple rule, one specifying that the agent avoid her own path, I think results become more interesting. This is called a self-avoiding walk. Self-avoiding walks are of interest in many domains, especially those sort that fill spaces. It is common for such an agent to quickly wall itself in, so getting it to fill a space can be a trick.
The Coding train has an excellent video on self-avoiding walks, and I highly recommend watching it, in part because you will see evidence of Shiffman’s code in my own, right down to naming my agent a Spot.
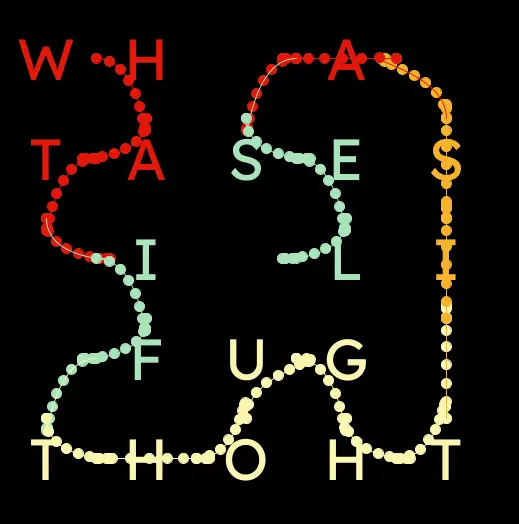
My idea was to make a recursive backtracking agent that would spell out a predetermined text along its path. This simply means that when my agent blocks itself in, it steps backward until the point where it has an option and explores that path instead.
The mechanics of a recursive backtracking self-avoiding agent are well described in the Shiffman video and I will not exhaust that discussion here and instead focus on the challenges my particular implementation brought, the first of which is directionality.
A typical implementation does care about direction in that it must keep an orderly stack of destinations visited, and it is easy enough to correspond each step of that journey with a character from a text (simply take the index of the current step on the stack and use that for an index from the source text), but if you simply display letters, reading the text becomes a real challenge, the result looking almost like a wordsearch.

My first thought was to differentiate words by color, which does work to some degree, but it does not help the reader find a start or ending point of the text.

An improvement, for sure, but insufficient.
Now some may consider this an inelegant solution, and I’m among them, but it occurred to me that I could simply point the way to the next letter and word with arrows. At first I concieved of arrows between words, but even this alone was insufficient, so I decided arrows between words and letters were necessary. This proved challenging indeed.
I settled for stemless arrows between letters, little “V”s but with the ends wider apart and the bottom point toward the next letter. So suddenly I have to know the side of the “cell” adjoining the next letter. I then need to orient my arrow toward the next cell specifically, so I also need to know the direction of that arrow, not just its space. To this end I settled for vectors representing the Object’s center position, and one representing the next letter’s center position.
When we create a new Agent we will immediately calculate and store where on the screen it’s center is, then when I have my path, I can refer to the center of each agent and it’s immediately following neighbor to determine a straight line between their centers.
Storing and calculating the current spot is determined by many factors, but for simplicity when I create the agent, I am simply giving it a row and column in a more abstract larger grid and then determining its real position based on other variables.
Spot(int x, int y) {
// the abstract position
pos = new IntVec(x, y);
// the drawabe center
realPos = new PVector(x * cellSize + padding, y * cellSize + padding);
// this is for path finding, ignore it.
options = allOptions();
}
Using a little vector scaling it then becomes easier to position two lines pointing in the desired direction:
void drawArrow(float x1, float y1, float x2, float y2) {
//line(x1, y1, x2, y2); picture a line going between the center of these two squares.
PVector vec = new PVector(x2 - x1, y2 - y1);
vec.mult(.62);
x2 = x1 + vec.x;
y2 = y1 + vec.y;
vec.setMag(8);
line(x2, y2, x2 - vec.x + vec.y, y2 - vec.y - vec.x);
line(x2, y2, x2 - vec.x - vec.y, y2 - vec.y + vec.x);
}
My original solution was to reach for translation and rotation to draw my arrow, but it was in that attempt that I learned something interesting. Consider this straightforward attempt to match crosshairs to a grid:
void setup() {
size(400, 400);
background(#FFFFFF);
float t = 0;
strokeWeight(.5);
for (int x = 0; x < 400; x+= 25) {
line(x, 0, x, height);
}
for (int y = 0; y < 400; y+= 25 ) {
line(0, y, width, y);
}
for (int x = 25; x < 350; x += 50) {
for (int y = 25; y < 350; y += 50 ) {
drawArrow(x, y, 10, t);
t += HALF_PI;
}
}
}
void drawArrow(float cx, float cy, float len, float angle){
// despite the function name I am drawing "plus" signs here.
pushMatrix();
stroke(255, 0, 0);
translate(cx, cy);
rotate(angle);
strokeWeight(1);
line(0, -len, 0, len);
line(-len, 0, len, 0);
strokeWeight(4);
popMatrix();
}

I apologize if you found that upsetting. The cause of this misalignment is the SMOOTH feature in processing and can be fixed with noSmooth(), but at the cost of considerably more jagged curves in my output. This was too high a price to pay. So vectors it was. Thank you Cave HEX of the Creative Coders discord channel for helping me understand the issue with noSmooth. Thank you noa of the same channel for help with the vector math to draw the arrows.
The next challenge was drawing the arrows between words. Simply using the same stemless arrows after a space was not sufficient. The real problem here was that the next word after a space could lie in any direction, so I needed a line traversing that blank space from it’s start to end, and that includes bends. This was far more challenging than I expected when setting out. Were it not for NKing at the same server, I would not have worked out the bezier curves.
My first issue was not understanding how to choose control points, as I kept ending up with no curve at all:

After a little more understanding and mastery I was arriving at the curves, but I wanted to interpolate the color to better indicate the transition that was being made, and that was not happening with the built in curve function:

So then I decided to use bezierPoint to find the points along the curve and color them individually, here was an early POC of merely following the path:
I could spend a day describing the issues I ran into trying to get this right. I spent a day actually doing it, after all. But please let me regale you, uncommented with debugging photos of the journey.

I’m trying!

I’m failing!
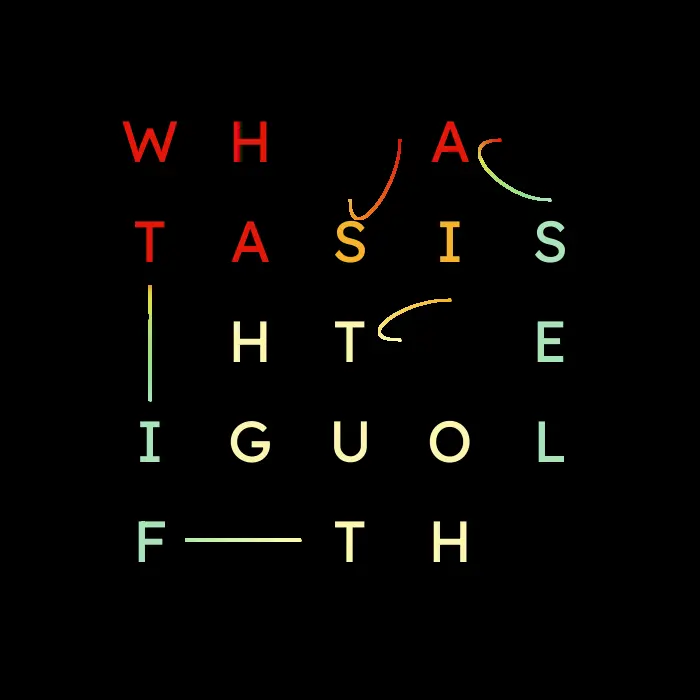
I won’t give up!

And as you can see, I’m getting there.
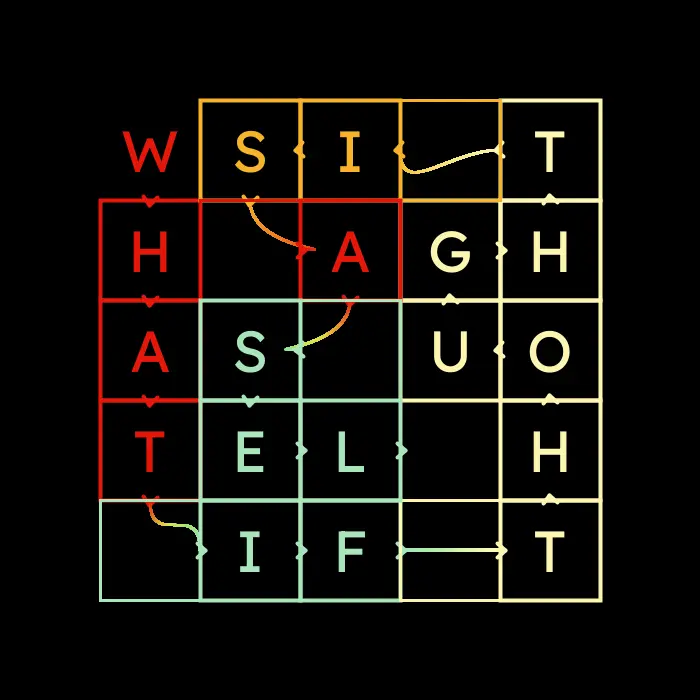
There are few words to describe how clear my intent was, but how troublesome it was to arrive upon satisfactory output, a situation I imagine many people have been in. You’ve been patient to get this far, but this is the code that ultimately got the curves I wanted, and it may not have happened without the help of NKing.
void drawConnection(Spot next) {
if (next.connector != null) {
int steps = 1000;
noFill();
strokeWeight(3);
for (int i = 0; i <= steps; i++) {
float t = i / float(steps);
color Curclr = lerpColor(clr, next.clr, map(i, 0, steps, 0, 1));
stroke(Curclr);
float x = bezierPoint(connector.x, connector.x + dir.x, next.connector.x + next.fromDir.x, next.connector.x, t);
point(x, y);
}
}
}
Most of the interesting work is done at this point. For many reasons, it made sense to first solve the walk, then using the ordered stack of points to go back after and fill out all the attributes (the coordinates of the current and next point, etc) that are needed to finally draw things.
It is worth pointing out that sometimes when I run my processing sketch, it just hangs. This is because finding long self-avoiding walks is a hard problem and recursive backtracking can take an impractically long time to find a long enough path for the text in the space I’ve provided for it.
Potential solutions?
1.) Hilbert Curve - Downside, too symmetrical, too efficient. This has the effect of making the output look exactly like a wordsearch.
2.) Maze generating algorithms - Not sequential enough, I might not get an orderly path at the end of it, unless I do recursive backtracking, but then again, too aggressive at filling the space.
3.) Dimerization - This was the most appealing solution.
However, and what a note on to end on, I simply didn’t care anymore! I’m fine just rerunning the program if the solution isn’t found quickly. Thank you for sticking with me through the journey. As always, source code, and final output:
