Polyjous

Starting with, as usual, a “what if”, the “if” in this case referring to the idea of tracing the perimeter of polygons instead of circles when generating a Lissajous Curve, I consulted with a very clever friend.

In short order and before he cooked dinner he provided a very helpful image:

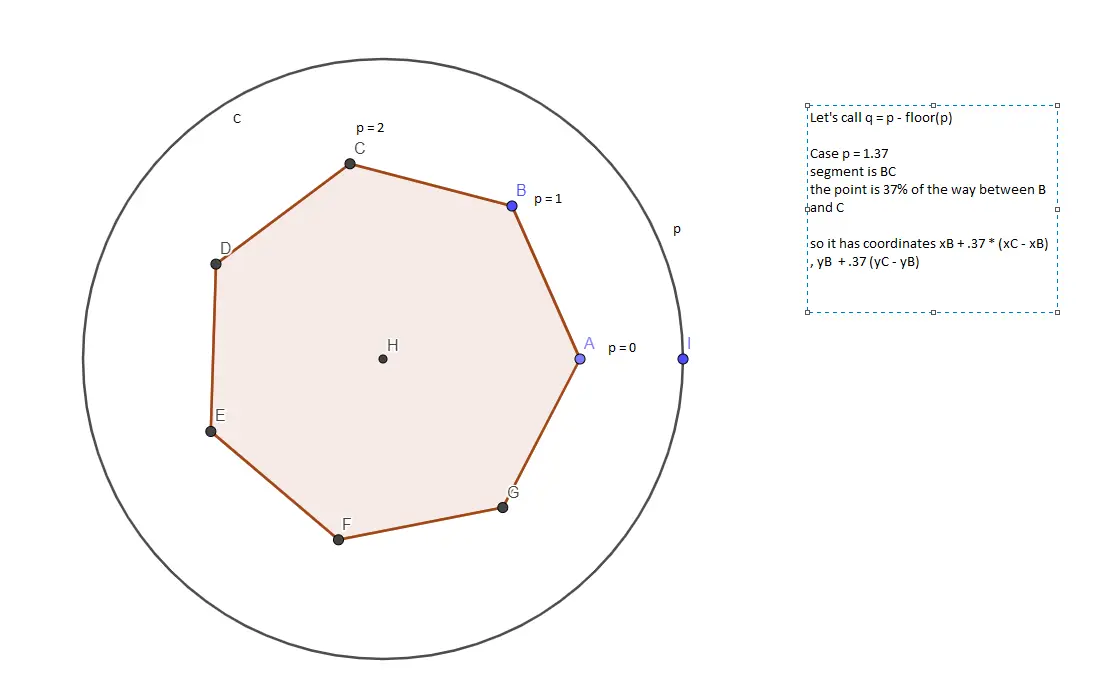
Some discussion and a little coding later we arrived at this function:

float polySin(float t, float n) {
  t = t % 360;
  t = t / 360f;
  t = t * n;
  float i = floor(t);   
  float q = t - floor(t);
  float[] p0 = segCoord(i, n);
  float[] p1 = segCoord(i + 1, n);
  
  float x = p0[0] + q * (p1[0] - p0[0]);  
  return x;
}

Please forgive the concision of this explanation, but what is happening here is I am taking two polygons, as in a traditional Lissajous set and I finding a point along the perimeter of each. I then project that point onto a unit circle by calling the above function for a given time, once to act a a sine, the other as a cosine. I plot the resultant position for that time, and iterate.

As you can see the results are very similar to the traditional figures, but I find that certain permutations allow you to see the angles of the polygons appear in a way that would never happen in the original set.